- 연관 포스팅(RB Tree 이론)
[Krafton Jungle | TIL_22.11.27] RB Tree 이론
균형 이진 탐색 트리(Balanced BST) 루트 노드로 부터 시작해서 찾고자하는 key 를 각 레벨에 따라 한번의 비교를 통해 key 값을 찾을 수 있다. $O(h)$ (h : 높이) 의 시간 복잡도를 가진다. insert, delete 연
olive-su.tistory.com
☁️ Overview
- 이진 트리의 특성을 기반으로 한다.
- RB Tree의 특성
- 모든 노드는 레드이거나 블랙이다.
- 루트는 블랙이다.
- 모든 리프는 블랙이다.
- 노드가 레드이면 그 노드의 자식은 모두 블랙이다.
- 각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 블랙 노드를 포함한다.
- ADT(Abstract Data Type) : ordered set, multiset
🔅 Intro
블랙 높이(black-height) : bh(x)
- 임의의 노드 x에서 리프까지 경로에 있는 모든 블랙 노드의 개수
- 자신은 제외한다.
동적 집합 연산
- $SEARCH$
- $MINIMUM$
- $MAXIMUM$
- $SUCCESSOR$
- $PREDECESSOR$
1. [CREATE] RB tree 구조체 생성
여러 개의 tree를 생성할 수 있어야 하며 각각 다른 내용들을 저장할 수 있어야 합니다.
대표 함수 : new_rbtree()
- 설명 : root 노드를 SENTINEL로 구현한다.
- 리턴 :
rbtree*생성한 구조체의 포인터
1-1. new_rbtree()
- source code
rbtree *new_rbtree(void)
{
rbtree *p = (rbtree *)calloc(1, sizeof(rbtree));
node_t *nil_node = (node_t *)calloc(1, sizeof(node_t));
nil_node -> color = RBTREE_BLACK;
p -> root = nil_node;
p -> nil = nil_node;
return p;
}
💡 경계 원소(Sentinel) : 한계 조건을 간단하게 해주는 더미 객체
- RB Tree에서 한계 조건을 다루기 편리하도록 NIL을 표현하기 위해 하나의 경계 노드(Sentienel)을 사용한다.
- 단말 노드는 모두 NIL이므로 단말 노드(NIL)로 연결되는 경우, 경계 노드(T.nil)로 연결되게끔 한다.
- 경계 노드(Sentinel)의 경우에도
node_t의 모든 필드를 가지지만, color필드만 블랙으로 지정한다. - 트리 내 각각의 NIL을 위해 개별적인 경계 노드를 사용하면 저장 공간이 낭비되므로, 트리 하나당 NIL node의 메모리 공간을 하나만 할당한다.
2. [INSERT] key 추가
구현하는 ADT가 multiset이므로 이미 같은 key의 값이 존재해도 하나 더 추가 합니다.
대표 함수(1) : rbtree_insert(tree, key)
- 설명 : key 값을 갖는 새로운 노드를 트리에 추가한다.
- 파라미터
rbtree*: 트리 포인터key_t: 새로 삽입하려는 키 값
- 리턴
node_t*: 삽입한 노드의 포인터
↳ 내부 함수(2) : rbtree_insert_fixup(tree, node)
- 설명 : 새로 노드를 삽입하는 과정에서 발생하는 규칙 위반을 교정한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 새로 삽입한 노드의 포인터
↳ 내부 함수(3) : left_rotate(tree, node)
- 설명 : 특정 node에 대한 left-rotation 연산 수행한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 노드 포인터
↳ 내부 함수(4) : right_rotate(tree, node)
- 설명 : 특정 node에 대한 right-rotation 연산 수행한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 노드 포인터
2-1. rbtree_insert(tree, key)
- source code
node_t *rbtree_insert(rbtree *t, const key_t key)
{
node_t *z = (node_t *)calloc(1, sizeof(node_t)); // key값을 갖는 노드를 새로 만든다.
z -> key = key; // node z : key 확정
node_t *y = t -> nil;
node_t *x = t -> root;
while(x != t -> nil){ // 리프의 부모 노드(NIL 직전 노드)까지 내려간다. (level : int(log N))
y = x;
if(z -> key < x -> key){
x = x -> left;
} else{
x = x -> right;
}
}
z -> parent = y; // 부모 노드 지정
if (y == t -> nil){ // 첫 번째 원소 삽입
t -> root = z;
} else if (z -> key < y -> key){ // 리프의 부모 노드가 key보다 작으면 왼쪽 자식으로 삽입
y -> left = z;
} else { // 리프의 부모 노드가 key보다 크거나 같으면 오른쪽 자식으로 삽입
y -> right = z;
}
z -> left = t -> nil;
z -> right = t -> nil;
z -> color = RBTREE_RED; // INSERT 규칙 적용 "새 노드 z를 삽입하고 해당 노드의 색상을 RED로 지정한다."
rbtree_insert_fixup(t, z);
return t -> root;
}- 새로 삽입하려는 노드에 대한 메모리 공간을 할당한다.
(node_t *)calloc - 리프의 부모 노드까지 내려간다.
- 새로 삽입하려는 노드의 키와 현재 내려온 노드(리프의 부모 노드)의 키를 비교하여 더 작으면 현재 노드의 왼쪽으로, 크거나 같으면 오른쪽으로 삽입한다.
- 이때, INSERT 함수의 구현 조건이 “구현하는 ADT가 multiset이므로 이미 같은 key의 값이 존재해도 하나 더 추가 합니다.”
이므로 같은 key값이 입력으로 들어올 수 있다. - 새로 삽입한 노드의 왼쪽 자식, 오른쪽 자식을 리프(NIL)로 연결한다.
- INSERT 규칙에 따라 새 노드의 색상을 RED로 지정한다.
- 무조건 새 노드의 색상을 RED로 지정하므로써 발생한 RB-Tree 의 규칙 위반을
rbtree_insert_fixup을 통해 해결한다.
2-2. rbtree_insert_fixup(tree, node)
- source code
void rbtree_insert_fixup(rbtree *t, node_t *z)
{
while (z -> parent -> color == RBTREE_RED){
// 부모가 조부모의 왼쪽 자식일 때
if (z -> parent == z -> parent -> parent -> left){
node_t *y = z -> parent -> parent -> right; // y is uncle.
// [CASE 1] : y is RED.
if (y -> color == RBTREE_RED){
z -> parent -> color = RBTREE_BLACK; // 부모 노드의 색을 블랙으로 바꾼다.
y -> color = RBTREE_BLACK; // 삼촌 노드의 색을 블랙으로 바꾼다.
z -> parent -> parent -> color = RBTREE_RED;
z = z -> parent -> parent;
} else {
// [CASE 2] : y is BLACK, z is right-child.
if (z == z -> parent -> right){
z = z -> parent;
left_rotate(t, z); // z가 오른쪽 자식이므로 왼쪽으로 회전을 수행한다.
}
// [CASE 3] : y is BLACK, z is left-child.
z -> parent -> color = RBTREE_BLACK;
z -> parent -> parent -> color = RBTREE_RED;
right_rotate(t, z -> parent -> parent); // z가 왼쪽 자식이므로 오른쪽으로 회전을 수행한다.
}
}
// 부모가 조부모의 오른쪽 자식일 때 (위의 로직과 동일)
else {
node_t *y = z -> parent -> parent -> left;
if (y -> color == RBTREE_RED){
z -> parent -> color = RBTREE_BLACK;
y -> color = RBTREE_BLACK;
z -> parent -> parent -> color = RBTREE_RED;
z = z -> parent -> parent;
} else{
if (z == z -> parent -> left){
z = z -> parent;
right_rotate(t, z);
}
z -> parent -> color = RBTREE_BLACK;
z -> parent -> parent -> color = RBTREE_RED;
left_rotate(t, z -> parent -> parent);
}
}
}
t -> root -> color = RBTREE_BLACK; // 특성 2(root : BLACK)에 대한 복구
}
- 조부모와 부모가 왼쪽-오른쪽의 경우가 대칭되므로,
(부모 == 조부모 -> left)와(부모 == 조부모 -> right)를 분기하여 진행한다.y를 부모의 형제, 삼촌 노드(uncle node)로 지정한다.- 이후 CASE 1 의 경우와 <CASE 2, CASE 3> 을 나눠서 조건문을 분기한다.
- CASE 1 와 <CASE 2, CASE 3> 는 상호 배타적이지만 CASE 2 와 CASE 3 는 상호 배타적이지않다.
- CASE 2 이후 CASE 3으로 연결된다.
2-3. left_rotate(tree, node)
- source code
void left_rotate(rbtree *t, node_t *x)
{
node_t *y = x -> right;
x -> right = y -> left; // y의 왼쪽 서브 트리를 x의 오른쪽 서브 트리로 옮긴다.
if (y -> left != t -> nil) { // y의 왼쪽 서브 트리의 부모를 연결한다.
y -> left -> parent = x;
}
y -> parent = x -> parent; // x의 부모를 y로 연결한다.
if (x -> parent == t -> nil){ // 트리 생성 후, 첫 노드 삽입
t -> root = y;
} else if (x == x -> parent -> left){ // x 노드가 부모 노드의 왼쪽 자식일 경우
x -> parent -> left = y;
} else { // x 노드가 부모 노드의 오른쪽 자식일 경우
x -> parent -> right = y;
}
y -> left = x; // x를 y의 왼쪽으로 놓는다.
x -> parent = y;
}
- y(x의 오른쪽 자식)에 대한 연결 작업을 수행한다.
- y의 레벨이 한 수준 낮아진다.(위로 올라감)
- x 노드를 y의 왼쪽 자식으로 연결한다.
- x의 레벨이 한 수준 높아진다.(아래로 내려감)
2-4. right_rotate(tree, node)
- source code
void right_rotate(rbtree *t, node_t *x)
{
node_t *y = x -> left;
x -> left = y -> right; // y의 오른쪽 서브 트리를 x의 왼쪽 서브 트리로 옮긴다.
if (y -> right != t -> nil) {
y -> right -> parent = x; // y 오른쪽 서브 트리의 부모에 x를 연결한다.
}
y -> parent = x -> parent; // y의 부모를 x로 연결한다.
if (x -> parent == t -> nil){ // 트리 생성 후, 첫 노드 삽입
t -> root = y;
} else if (x == x -> parent -> right){ // x 노드가 부모 노드의 오른쪽 자식일 경우
x -> parent -> right = y;
} else { // x 노드가 부모 노드의 왼쪽 자식일 경우
x -> parent -> left = y;
}
y -> right = x; // x를 y의 오른쪽으로 놓는다.
x -> parent = y;
}
left_rotate에서 left ↔ right 만 바꿔서 구현한다.- y(x의 왼쪽 자식)에 대한 연결 작업을 수행한다.
- y의 레벨이 한 수준 낮아진다.(위로 올라감)
- x 노드를 y의 오른쪽 자식으로 연결한다.
- x의 레벨이 한 수준 높아진다.(아래로 내려감)
3. [FIND] RB Tree내에 key가 있는지 탐색
- RB tree내에 해당 key가 있는지 탐색하여 있으면 해당 node pointer 반환
- 해당하는 node가 없으면 NULL 반환
대표 함수 : rbtree_find(tree, key)
- 설명 : 이진 검색 트리의 SEARCH 연산을 그대로 적용한다.
- 파라미터
rbtree*: 트리 포인터key_t: 찾으려는 키 값
- 리턴
node_t*: 찾은 노드의 포인터
3-1. rbtree_find(tree, key)
- source code
node_t *rbtree_find(const rbtree *t, const key_t key)
{
node_t *x = t -> root; // 시작 노드를 루트로 지정
while (x != t -> nil && key != x -> key){
if (key < x -> key){ // 찾으려는 키가 현재 노드의 키 값보다 작으면 왼쪽 자식 탐색
x = x -> left;
} else {
x = x -> right; // 찾으려는 키가 현재 노드의 키 값보다 크면 오른쪽 자식 탐색
}
}
if (x == t -> nil) { // 만약 찾으려는 key가 트리에 없으면 NULL 리턴
return NULL;
}
return x;
}
- 탐색 시작 위치를 루트로 지정한다.
- 반복문
- 찾는 key와 동일한 키 값이 나오면 해당 노드를 리턴한다.
- 만약 찾는 key가 트리내에 존재하지 않는 다면
NULL을 리턴한다.
4. [MIN] RB Tree의 최소 값 탐색
최소 값을 가진 node pointer 반환
대표 함수 : rbtree_min(tree)
- 설명 : RB Tree에서 가장 작은 값을 반환한다.
- 파라미터
rbtree*: 트리 포인터
- 리턴
node_t*: 찾은 노드의 포인터
4-1. rbtree_min(tree)
- source code
node_t *rbtree_min(const rbtree *t)
{
node_t *x = t -> root; // 시작 노드를 루트로 지정
while (x -> left != t -> nil)
x = x -> left; // 왼쪽 자식을 순환적으로 반복 탐색하며 가장 작은 값 탐색
return x;
}
- 시작 노드를 루트로 지정한다.
- 왼쪽 자식을 순환적으로 반복 탐색하며 트리 전체에서의 가장 작은 값을 탐색한다.
- 이진 트리 특성상 부모 노드보다 작은 값이 왼쪽 자식에 위치하므로 리프를 만날 때까지 반복하면 가장 작은 값을 찾을 수 있다.
5. [MAX] RB Tree의 최대 값 탐색
최대 값을 가진 node pointer 반환
대표 함수 : rbtree_max(tree)
- 설명 : RB Tree에서 가장 큰 값을 반환한다.
- 파라미터
rbtree*: 트리 포인터
- 리턴
node_t*: 찾은 노드의 포인터
5-1. rbtree_max(tree)
- source code
node_t *rbtree_max(const rbtree *t)
{
node_t *x = t -> root; // 시작 노드를 루트로 지정
while (x -> right != t -> nil)
x = x -> right; // 오른쪽 자식을 순환적으로 반복 탐색하며 가장 큰 값 탐색
return x;
}
- 시작 노드를 루트로 지정한다.
- 오른쪽 자식을 순환적으로 반복 탐색하며 트리 전체에서의 가장 큰 값을 탐색한다.
- 이진 트리 특성상 부모 노드보다 큰 값이 오른쪽 자식에 위치하므로 리프를 만날 때까지 반복하면 가장 큰 값을 찾을 수 있다.
6. [ERASE] 특정 노드 하나 삭제
RB tree 내부의 ptr로 지정된 node를 삭제하고 메모리 반환
대표 함수(1) : rbtree_erase(tree, node)
- 설명 : 트리에서 특정 노드 하나를 삭제한다.
- 파라미터
rbtree*: 트리 포인터key_t: 노드 포인터
- 리턴
int: 성공 시 0
↳ 내부 함수(2) : rbtree_successor(tree, node)
- 설명 : 직후 원소(successor)를 탐색한다.
- 파라미터
rbtree*: 트리 포인터node_t*: successor를 찾고자 하는 노드
- 리턴
node_t*: successor 노드의 포인터
↳ 내부 함수(3) : rbtree_erase_fixup(tree, node)
- 설명 : 노드 삭제 과정에서 발생하는 규칙 위반을 교정한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 삭제한 노드
↳ 내부 함수(4) : rbtree_transplant(tree, node, node)
- 설명 : 서브 트리 A를 서브트리 B로 교체한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 서브 트리 A의 루트 노드node_t*: 서브 트리 B의 루트 노드
↳ 내부 함수(5) : left_rotate(tree, node)
- 설명 : 특정 node에 대한 left-rotation 연산 수행한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 노드 포인터
↳ 내부 함수(6) : right_rotate(tree, node)
- 설명 : 특정 node에 대한 right-rotation 연산 수행한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 노드 포인터
6-1. rbtree_erase(tree, node)
- source code
int rbtree_erase(rbtree *t, node_t *p)
{
if (p == NULL){
return 0;
}
node_t *x; // y의 원래 위치로 이동하는 노드
node_t *y = p; // y를 삭제하려는 노드 p로 지정한다.
color_t y_original_color = y -> color; // CASE 1. 삭제색 : 삭제되는 노드의 색상
// [CASE 1] p가 하나 이하의 자식을 가지고 있을 때
// 단순히 하나 또는 nil(자식이 없음) 서브 트리의 레벨을 현재 삭제하려는 노드 위치로 올린다.
if (p -> left == t -> nil){
x = p -> right;
rbtree_transplant(t, p, p -> right);
} else if (p -> right == t -> nil){
x = p -> left;
rbtree_transplant(t, p, p -> left);
// [CASE 2] p가 두 개의 자식을 가지고 있을 때
} else {
y = rbtree_successor(t, p); // p가 삭제되고 p의 위치로 올 노드
y_original_color = y -> color; // CASE 2. 삭제색 : successor의 색상
x = y -> right; // y의 오른쪽 자식
if (y == p -> right){ // p의 오른쪽 자식이 왼쪽 서브 트리를 가지고 있지않은 경우
x -> parent = y;
} else { // p의 오른쪽 자식이 왼쪽 서브 트리를 가지고 있는 경우
rbtree_transplant(t, y, y -> right); // successor의 서브 트리를 분리한다.
y -> right = p -> right;
y -> right -> parent = y;
}
rbtree_transplant(t, p, y); // 삭제하려는 노드의 오른쪽 자식으로 successor를 붙인다.
y -> left = p -> left;
y -> left -> parent = y;
y -> color = p -> color;
}
if (y_original_color == RBTREE_BLACK){ // 삭제되는 색이 블랙이면 재조정을 한다.
rbtree_erase_fixup(t, x);
}
free(p); // p에 할당되어있던 메모리를 해제해준다.
p = NULL; // dangling pointer를 방지하기 위해 해제된 포인터 값으로 NULL을 넣어준다.
return 0;
}
- 삭제하려는 노드(p)를
y로 지정한다.
1. 삭제하려는 노드가 자식이 없거나 하나의 자식만 있으면 서브 트리의 레벨만 현재 노드의 위치로 롤린다.
- 삭제 색 : 기존에 삭제하려던 노드의 색
2. 삭제하려는 노드가 두 개의 자식을 가지고 있을 때
successor가 노드를 삭제하면 해당 위치로 오게된다.- 삭제 색 :
successor의 색 successor를 삭제하려는 노드(p)의 위치로 올려야하기 때문에 연관 서브 트리들에 대한 TRANSPLANT 연산을 수행한다.
- 이후 삭제되는 색상이 블랙이면 RB-Tree 규칙 위반이 발생하므로
rbtree_erase_fixup을 통해 해결한다.
6-2. rbtree_successor(tree, node)
- source code
node_t *rbtree_successor(rbtree *t, node_t *x)
{
node_t *y = x -> right; // y는 x의 오른쪽 자식
while (y -> left != t -> nil) { // 리프 이전까지 반복
y = y -> left; // y에 y의 왼쪽 자식을 연속해서 갱신
}
return y;
}- x의 successor를 찾기 위해 오른쪽 서브트리의 왼쪽 자식을 반복해서 탐색을 진행 한다.
6-3. rbtree_erase_fixup(tree, node)
- source code
void rbtree_erase_fixup(rbtree *t, node_t *x)
{
node_t *w;
while (x != t -> root && x -> color == RBTREE_BLACK){
if (x == x -> parent -> left) { // x가 왼쪽 자식일 때
w = x -> parent -> right; // w is sibling.
// [CASE 1] w is RED.
if (w -> color == RBTREE_RED){
w -> color = RBTREE_BLACK; // w와 p의 색을 바꾼다.
x -> parent -> color = RBTREE_RED;
left_rotate(t, x -> parent); // p를 기준으로 left-rotate를 수행한다.
w = x -> parent -> right;
}
// [CASE 2] w is BLACK, w's children are BLACK.
if (w -> left -> color == RBTREE_BLACK && w -> right -> color == RBTREE_BLACK){
w -> color = RBTREE_RED; // w를 레드로 바꾼다.
x = x -> parent;
} else {
// [CASE 3] w is BLACK, w's left-child is RED, w's right-child is BLACK.
if (w -> right -> color == RBTREE_BLACK) {
w -> left -> color = RBTREE_BLACK; // w와 w의 왼쪽 자식의 색을 바꾼다.
w -> color = RBTREE_RED;
right_rotate(t, w); // w를 기준으로 right-rotate를 수행한다.
w = x -> parent -> right;
}
// [CASE 4]
w -> color = x -> parent -> color; // w와 p의 색을 바꾼다.
x -> parent -> color = RBTREE_BLACK;
w -> right -> color = RBTREE_BLACK; // p를 기준으로 left-rotate를 수행한다.
left_rotate(t, x -> parent);
x = t -> root;
}
} else { // x가 오른쪽 자식일 때 (위의 로직과 동일)
w = x -> parent -> left;
if (w -> color == RBTREE_RED){
w -> color = RBTREE_BLACK;
x -> parent -> color = RBTREE_RED;
right_rotate(t, x -> parent);
w = x -> parent -> left;
}
if (w -> right -> color == RBTREE_BLACK && w -> left -> color == RBTREE_BLACK){
w -> color = RBTREE_RED;
x = x -> parent;
} else {
if (w -> left -> color == RBTREE_BLACK) {
w -> right -> color = RBTREE_BLACK;
w -> color = RBTREE_RED;
left_rotate(t, w);
w = x -> parent -> left;
}
w -> color = x -> parent -> color;
x -> parent -> color = RBTREE_BLACK;
w -> left -> color = RBTREE_BLACK;
right_rotate(t, x -> parent);
x = t -> root;
}
}
}
x -> color = RBTREE_BLACK;
}
- x가 왼쪽 자식인 경우-오른쪽 자식인 경우가 대칭되므로,
(x == parent -> left)와(x == parent -> right)를 분기하여 진행한다.w를 형제 노드(sibling node)로 지정한다.- 이후 CASE 1 에서 CASE 2 또는 <CASE 3, CASE 4> 로 이어질 수 있다.
6-4. rbtree_transplant(tree, node, node)
- source code
void rbtree_transplant(rbtree *t, node_t *u, node_t *v)
{
if (u -> parent == t -> nil){ // u가 루트 노드일 떄
t -> root = v;
} else if (u == u -> parent -> left) { // u가 왼쪽 자식일 때
u -> parent -> left = v;
} else {
u -> parent -> right = v; // u가 오른쪽 자식일 때
}
v -> parent = u -> parent; // v의 부모 연결
}
- 노드 u를 삭제하기 위해 노드 u의 서브 트리들과 u의 부모를 v에 연결한다.
6-5, 6-6. left_rotate(tree, node), right_rotate(tree, node)
- 2-3, 2-4와 동일하다.
7. [DELETE] 트리 전체 삭제
- RB tree 구조체가 차지했던 메모리 반환
- 해당 tree가 사용했던 메모리를 전부 반환해야 합니다.
대표 함수(1) : delete_rbtree(tree)
- 설명 : RB tree 구조체 자체의 메모리를 반환한다.
- 파라미터
rbtree*: 트리 포인터
↳ 내부 함수(2) : delete_inner_node(tree, node)
- 설명 : 특정 node에 대한 left-rotation 연산 수행한다.
- 파라미터
rbtree*: 트리 포인터node_t*: 노드 포인터
7-1. delete_rbtree(tree)
- source code
void delete_rbtree(rbtree *t)
{
delete_inner_node(t, t -> root); // 연결된 내부 노드들 모두 제거
free(t -> nil); // 내부 노드 모두 삭제 후, NIL 노드 해제
t -> nil = NULL;
free(t); // RB tree 구조체 자체 해제
t = NULL;
}
- 트리 전체에 할당된 메모리를 해제한다.
- 서브 트리들에 대한 메모리 해제를 해줘야한다.
7-2. delete_inner_node(tree)
- source code
void delete_inner_node(rbtree *t, node_t *x)
{
if (x != t -> nil){
delete_inner_node(t, x -> left); // 왼쪽 자식들 모두 제거
delete_inner_node(t, x -> right); // 오른쪽 자식들 모두 제거
free(x); // 단말 노드 : 메모리 해제
x = NULL;
}
}
- 왼쪽 서브 트리와, 오른쪽 서브 트리에 대해 재귀적으로 메모리를 해제한다.
- 이후, 단말 노드에 다다르면 해당 노드의 메모리를 해제한다.
8. [TRAVERSAL] 트리 중위 순회
- RB tree의 내용을 key 순서대로 주어진 array로 변환
- array의 크기는 n으로 주어지며 tree의 크기가 n 보다 큰 경우에는 순서대로 n개 까지만 변환
- array의 메모리 공간은 이 함수를 부르는 쪽에서 준비하고 그 크기를 n으로 알려줍니다.
대표 함수(1) : rbtree_to_array(tree, arr, size)
- 설명 : 중위 순회 결과를 배열에 담는다.
- 파라미터
rbtree*: 트리 포인터key_t*: 중위 순회 결과를 저장할 배열size_t: 배열의 사이즈
↳ 내부 함수(2) : inorder_tree_walk(node, arr, tree, idx)
- 설명 : RB tree의 노드들을 중위 순회한다.
- 파라미터
node_t*: 루트 노드key_t*: 중위 순회 결과 배열rbtree*: 트리 포인터idx: 배열에 저장할 위치
- 리턴
int: 배열의 인덱스
8-1. rbtree_to_array(tree, arr, size)
- source code
int rbtree_to_array(const rbtree *t, key_t *arr, const size_t n)
{
node_t *x = t->root;
inorder_tree_walk(x, arr, t, 0);
return 0;
}
- 중위 순회 결과를 파라미터로 들어온 배열에 저장한다.
8-2. inorder_tree_walk(node, arr, tree, idx)
- source code
int inorder_tree_walk(node_t *p, key_t *arr, const rbtree *t, int i)
{
if (p == t -> nil) {
return i;
}
i = inorder_tree_walk(p -> left, arr, t, i);
arr[i++] = p -> key; // 인덱스를 하나씩 올려가며 중위 순회 결과를 배열에 담는다.
i = inorder_tree_walk(p -> right, arr, t, i);
return i;
}
- 이진 트리의 특성 상, 중위 순회를 진행하면 키 값을 오름차순으로 정리한 결과를 얻을 수 있다.
- 왼쪽 서브 트리가 부모 노드 보다 무조건 작고 오른쪽 서브 트리가 부모 노드 보다 무조건 크다.
🙌🏻 보충 설명
1. 회전(Rotation)
👉 관련 내용 : 2-3, 2-4
- 시간복잡도 $O(1)$
- 레드 블랙 트리의 특성을 복구하기 위해 트리내의 일부 노드들의 색과 포인터를 변경해주는 연산
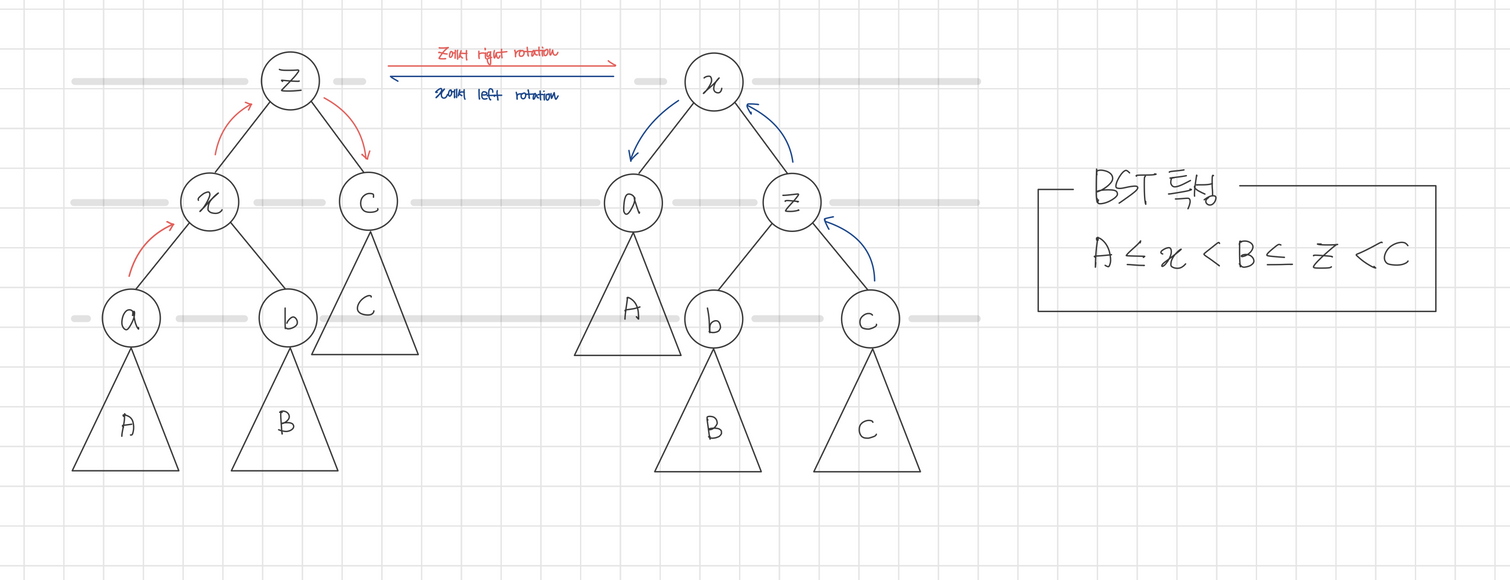
- TREE-INSERT 나 TREE-DELETE 는 트리를 수정하므로 트리 수정시, 레드 블랙 트리의 특성을 위반할 수가 있다.
- 이진 검색 트리의 특성을 보전해주는 연산이다.
- 트리의 균형을 맞추기 위해 수행한다.
- 회전을 통해 포인터만 변경되며 다른 필드는 그대로 유지된다.
- LEFT-ROTATE와 RIGHT-ROTATE는 서로 대칭이다.
2. 삽입(Insertion)
👉 관련 내용 : 2-1
- 시간복잡도 $O(lgn)$
- 새 노드 z를 삽입하고 해당 노드의 색상을 RED로 지정한다.
- 이후 교정 작업을 수행하여 RB Tree의 특성을 유지한다.
🌲 메인 함수) INSERT
- BST Pseudocode
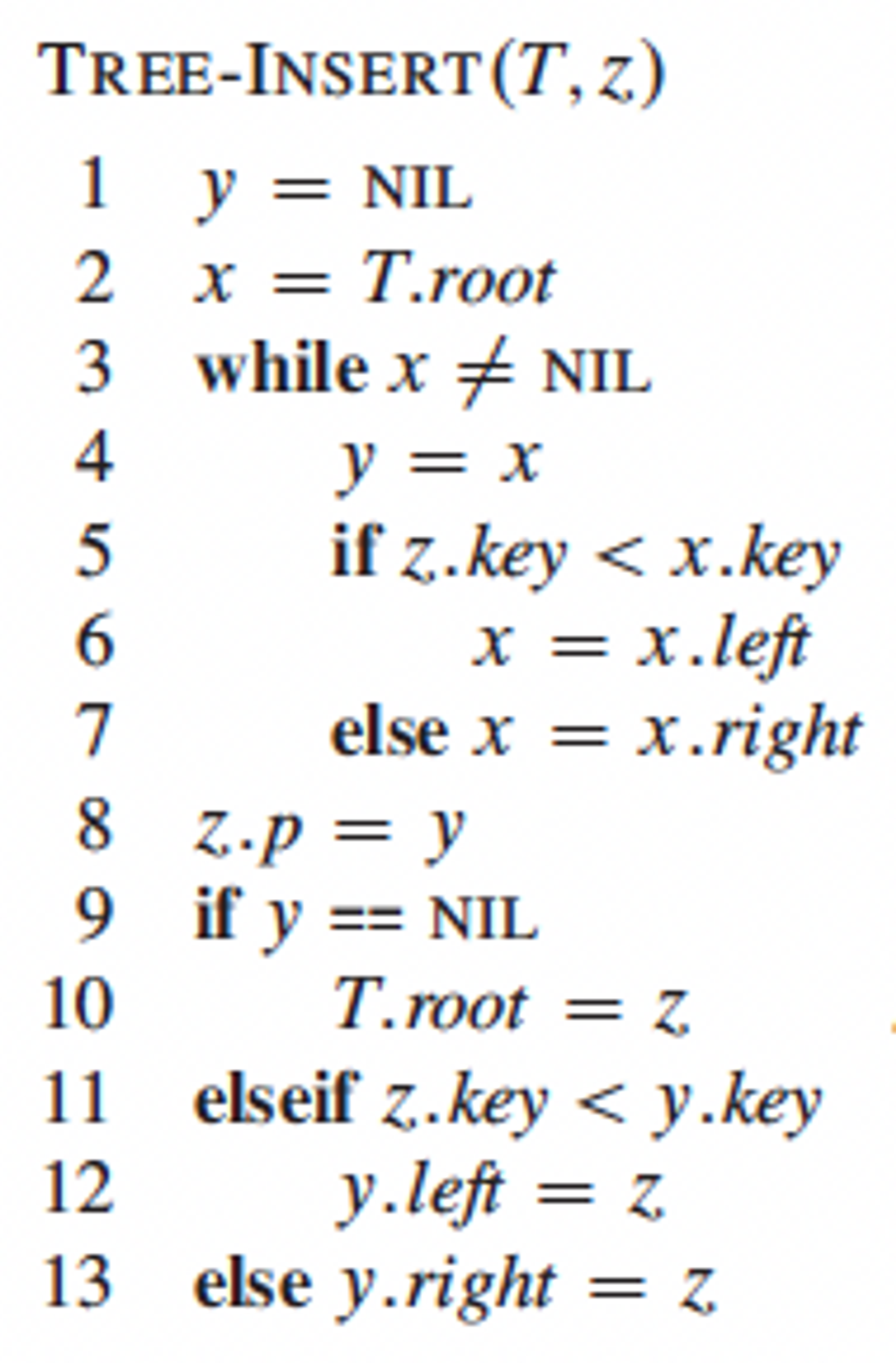
- RBT Pseudocode
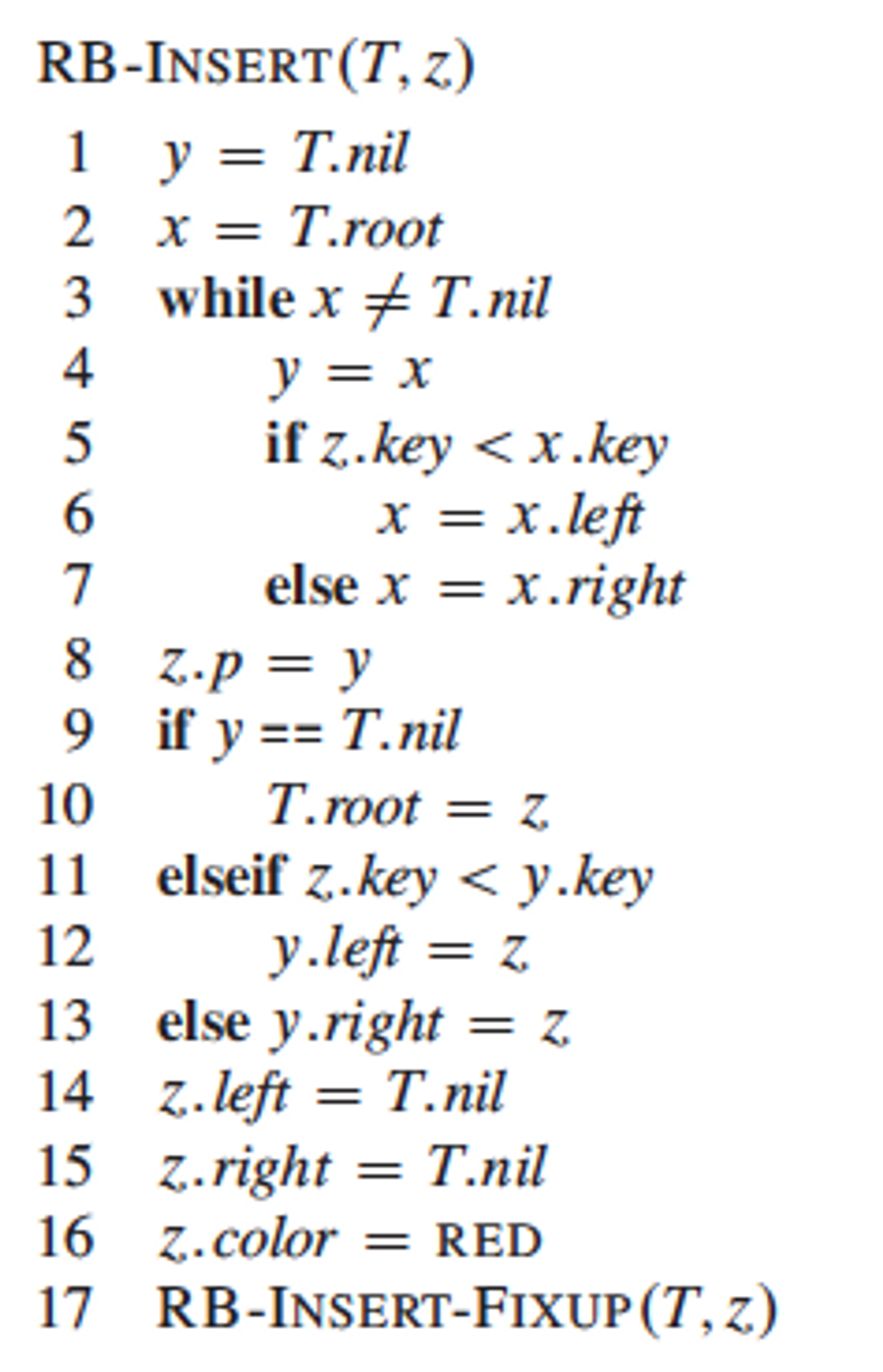
TREE-INSERT 🆚 RB-INSERT
1. (BST) NIL → (RBT) T.nil
2. z.left, z.right = T.nil, T.nil
3. 노드 z의 색상 : 레드
4. 3번 사항이 RB Tree 규칙을 위반할 수 있으므로 RB-INSERT-FIXUP 호출
🌲 서브 함수) RB-INSERT-FIXUP
- RB-INSERT-FIXUP

📜 RB Tree 규칙 위반 사항
- 삽입 노드를 무조건 레드 노드로 설정하기 때문에 생긴다.
- 특성 2️⃣ : “루트는 블랙이다.”
- z가 루트일 때 위반된다.
- 특성 4️⃣ : ”노드가 레드이면 그 노드의 자식은 모두 블랙이다.”
- z의 부모가 레드일 때 위반된다.

1. while 루프
- CASE 를 나누어, 노드 삽입 이후 RB Tree 규칙 위반 사항에 대한 조정을 하며 while문을 반복하면서 루트 노드까지 올라간다.
- z의 포인터가 점점 올라가면서 RB Tree 규칙 위반 사항을 조정한다.
- 노드
z는 레드이다. z → parent == z → root면,z → parent는 블랙이다.
- 특성 2️⃣가 위반되는 전제 조건 : z는 루트이며 레드이다. (❌)
- 특성 4️⃣가 위반되는 전제 조건 :
z와z → parent가 모두 레드이다. (❌)
z -> parent가 레드일 때만 루프 수행하므로 while루프 내에서 특성 4를 위반하는 지 판단한다.- 총 6가지 경우에 대해서 판단을 하면 되는데, ‘조부모-부모’가 ‘왼쪽-오른쪽’의 경우가 대칭된다.
2. CASE 1, 2, 3
- 해당 노드의 삽입이 RB Tree의 특성을 위반하는 지 3가지 경우로 나눠서 살펴본다.
- 총 6가지이지만 ‘조부모-부모’가 ‘왼쪽-오른쪽’ 의 경우가 대칭으로 동일하므로 한쪽의 3가지 경우에 대해서만 적었다.

⚠️ (a)와 (b)는 각각 ‘조부모-부모’가 ‘왼쪽-오른쪽’의 경우에 대한 대칭을 나타냈으므로 상하 동일한 로직으로 수행된다.

- CASE 1
- 부모(A)와 삼촌(D)이 레드이므로 블랙으로 바꿔준다.
- 다음 while 루프를 위해
z의 포인터를 조부모(C)로 바꿔준다. - 다시 새로운
z(C)에 대해 특성 4️⃣에 대한 위반 여부를 파악하기 위해 새로운z(C)의 색을 레드로 바꿔주고 while 루프를 다시 돈다.
- CASE 2
- 부모와 자식의 레벨을 바꾸고 LEFT-ROTATE 를 수행한다.
- 여전히 부모
z → parent와 자식z이 모두 레드이다. 특성 4️⃣ (❌)- CASE 3 의 경우와 동일해진다. → CASE 3으로 연결
- CASE 3
- 부모와 조부모의 색상을 바꾼다.
- Before(부모, 조부모) : 레드, 블랙
- After(부모, 조부모) : 블랙, 레드
- 이후 RIGHT-ROTATE 를 수행한다.
- 부모와 조부모의 색상을 바꾼다.
3. 탐색(Searching)
👉 관련 내용 : 3
- BST Pseudocode

- 시간복잡도 $O(n)$
- 이진 검색 트리의 특성을 이용해서, k가 x.key보다 작으면 검색은 왼쪽 서브 트리를 대상으로,
크면 오른쪽 서브 트리를 대상으로 검색을 계속 진행한다. - 재귀와 순환적 방법 두 가지로 구현할 수 있지만 대부분의 경우에 순환적 형태의 버전이 더 빠르다.
4. 삭제(Deletion)
👉 관련 내용 : 6
- 시간복잡도 $O(lgn)$
- 이진 탐색 트리에서의 노드 삭제 과정과 동일하지만, 노드를 삭제한 후 레드블랙 특성을 복구하기 위한 색깔 변경 및 회전 등이 일어난다.
rbtree_erase_fixup
🌲 서브 함수 1) TRANSPLANT
- BST Pseudocode

- RBT Pseudocode

- TRANSPLANT 🆚 RB-TRANSPLANT
- 1. (BST) NIL → (RBT) T.nil
- 2. (TRANSPLANT. line 6 ~ 7) 조건 O → (RB-TRANSPLANT. line 6) 조건 X
- u가 nil일 때도 v → parent에 값을 할당할 수 있다.
🌲 서브 함수 2) SUCCESSOR
- Pseudocode

- 노드 x의 직후 원소를 찾는다.
💡 직후 원소(successor) : x.key 보다 큰 키 중 가장 작은 키를 가지는 노드
- 오른쪽 서브 트리가 비어 있지 않으면 x의 직후 원소는 오른쪽 서브 트리의 제일 왼쪽 노드가 된다.
🌲 메인 함수) DELETE
- BST Pseudocode

- RBT Pseudocode

TREE-DELETE 🆚 RB-DELETE
1. RB-DELETE의 기본 구조는 TREE-DELETE와 같다.
2-1. z가 하나 이하의 자식을 가지고 있을 때
- 단순히 z를 트리에서 삭제하고 y를 z로 설정한다.
2-2. z가 두 개의 자식을 가지고 있을 때
- y는 z의 직후 원소가 된다.
- y는 z의 위치로 이동한다.
- y가 이동하기 전 색깔(y’s Before Color)과 y의 원래 위치로 이동하는 x도 관리한다.
- 삭제 색을 결정해야한다.
- CASE 1. 삭제되는 노드가 하나 이하의 자식을 가지고 있을 때는 삭제되는 노드의 색이 삭제색이 된다.
- CASE 2. 삭제되는 노드가 두 개의 자식을 가지고 있을 때는 successor의 색이 삭제색이 된다.
- 만약 삭제색이 블랙이면 RB Tree 규칙을 위반할 수 있으므로 RB-ERASE-FIXUP 호출
🌲 서브 함수3) RB-ERASE-FIXUP
- RB-ERASE-FIXUP

📜 RB Tree 규칙 위반 사항
- 삭제 색이 레드이면, 규칙을 위반하지 않는다.
- 삭제 색이 블랙이면 특성 2️⃣, 특성 4️⃣, 특성 5️⃣ 를 위반할 수있다.
- 특성 2️⃣ : “루트는 블랙이다.”
- 루트 노드가 삭제될 경우 발생할 수 있다.
- 특성 4️⃣ : ”노드가 레드이면 그 노드의 자식은 모두 블랙이다.”
- 블랙 노드가 삭제되면서 레드 노드가 연속될 수 있다.
- 특성 5️⃣ : ”각 노드로부터 그 노드의 자손인 리프로 가는 경로들은 모두 같은 수의 블랙 노드를 포함한다.”
- 블랙 노드가 지워졌을 때, 블랙 노드의 높이가 -1이 된다.
1. while 루프
- CASE 를 나누어, 블랙 노드 삭제 시 발생할 수 있는 RB Tree 규칙 위반 사항에 대한 조정을 하며 while문을 반복하면서 루트 노드까지 올라간다.
x의 포인터가 점점 올라가면서 RB Tree 규칙 위반 사항을 조정한다.
- 타겟 노드
x는 항상 루트가 아닌 이중 흑색 노드를 가리킨다. - 총 8가지 경우에 대해서 판단을 하면 되는데,
x가 부모의 ‘왼쪽 자식’인지 ‘오른쪽 자식’인지의 경우가 대칭된다.
delete_fixup은 특성 5️⃣를 보존하는 과정이다.- ∴ 이전 CASE 들에서 특성 5️⃣를 계속 만족했다면 그 다음 CASE들에서도 만족한다.
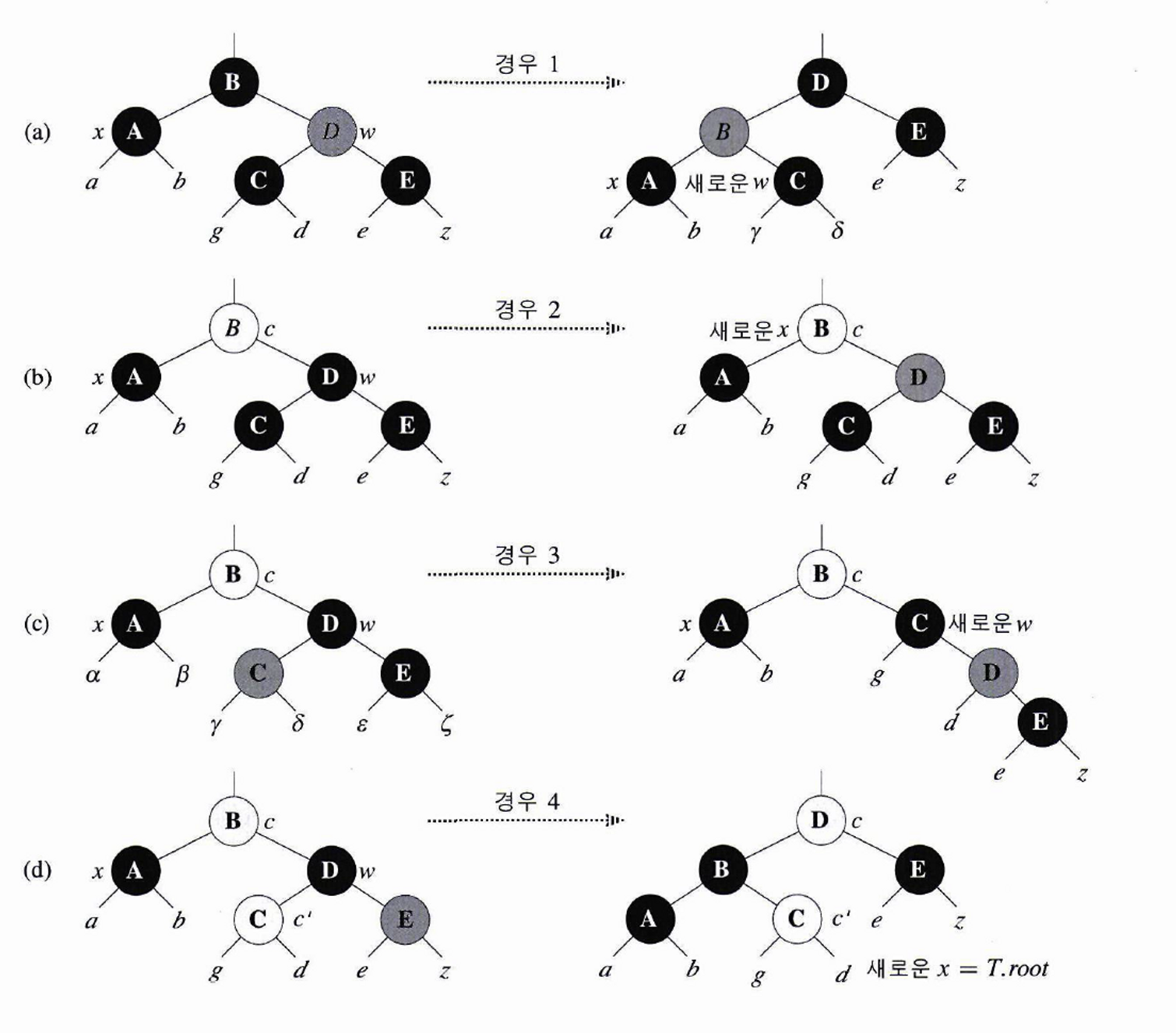
2. CASE 1, 2, 3, 4
- 블랙 노드 삭제 시 발생하는 특성 5️⃣ 위반의 경우를 4가지로 나눠서 살펴본다.
- 총 8가지이지만 ‘p(parent)-x(삭제하려는 노드)’ 관계가 ‘왼쪽-오른쪽’ 의 경우가 대칭으로 동일하므로 왼쪽 자식의 4가지 경우에 대해서만 적었다.
📢 x : 삭제할 노드, w : 형제 노드 , p : x 의 부모 노드
- CASE 1 :
w가 레드인 경우w와p의 색을 바꾼다.p를 기준으로 LEFT-ROTATE 를 수행한다.- 👉 이후, CASE 1은 CASE 2 또는 CASE 3 또는 CASE 4 로 이어진다.
- CASE 2 :
w가 블랙이고w의 자식들이 모두 블랙인 경우w에서 블랙을 제거하고 레드로 설정한다.p를 새로운x로 두고while를 다시 수행한다.
- CASE 3 :
w는 블랙,w의 왼쪽 자식은 레드,w의 오른쪽 자식은 블랙인 경우w와 왼쪽 자식w.left의 색을 바꾼다.w를 기준으로 RIGHT-ROTATE 를 수행한다.- 👉 이후, CASE 3은 CASE 4 로 이어진다.
- CASE 4 :
w는 블랙,w의 오른쪽 자식은 레드인 경우w와p의 색을 바꾼다.p를 기준으로 LEFT-ROTATE 를 수행한다.
🔗 Reference
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein - Introduction to Algorithms-The MIT Press
'🌱 Dev Diary > 📄 TIL' 카테고리의 다른 글
| Malloc Lab 구현 (0) | 2022.12.08 |
|---|---|
| Team Session - Data Segment (0) | 2022.12.08 |
| RB Tree 이론 (1) | 2022.11.29 |
| C 정복하기(2) - 메모리 할당 (0) | 2022.11.28 |
| C 정복하기(1) - 포인터 (0) | 2022.11.28 |
