728x90
☑️ To-do
- 정렬 알고리즘 정리하기
- 주요 정렬 알고리즘 안보고 코딩 해보기
- ✔️ 버블 정렬
- ✔️ 삽입 정렬
- ✔️ 선택 정렬
- ✔️ 셸 정렬
- ✔️ 퀵 정렬
- ✔️ 도수 정렬
- CSAPP Ch 1.6 까지 정리하기
1. 버블 정렬
- 루프를 돌면서 인접 데이터간 대소 관계 비교 후, swap 연산 수행
- 루프가 하나씩 돌 때마다 오른쪽 원소가 정렬된다.
- 서로 이웃한 원소만 교환하므로 안정적이다.
def bubble_sort(array):
for i in range(len(array)):
for j in range(len(array) - 1 - i):
if array[j] > array[j + 1]:
array[j], array[j + 1] = array[j + 1], array[j]
return array
- 뒤에서 부터 정렬된 데이터를 채워나감
알고리즘 개선 1 : swap 횟수
- 배열의 정렬 상태에 따라 종료 시점을 결정한다.
- 만약, swap 연산이 한번도 안 이루어진다면 이미 정렬이 끝난 배열이므로 그 즉시 정렬을 끝내도 된다.
arr = [42, 32, 24, 60, 15]
def bubble_sort(array):
for i in range(len(array)):
cnt = 0 # 배열 내 원소 교환 횟수를 저장
for j in range(len(array) - 1 - i):
if array[j] > array[j + 1]:
cnt += 1
array[j], array[j + 1] = array[j + 1], array[j]
if not cnt: break # 교환 횟수가 0이라면 이미 정렬된 배열이므로 정렬 종료
return array
print(bubble_sort(arr))
알고리즘 개선 2 : scan 범위 제한
def bubble_sort(array):
for i in range(len(array)):
k = 0
# 스캔 범위 제한
while k < len(array) - 1:
for j in range(k, n - 1 - i):
if array[j] > array[j + 1]:
last = j
array[j], array[j + 1] = array[j + 1], array[j]
k = last
return array
반복문의 첫 번째 루프를 모두 돌고나면, 맨 마지막 원소에 가장 큰 값이 저장되게 된다.
- 이때 array[0] ~ array[4] 까지는 교환 ❌

이러한 무의미한 교환 과정은 다음 루프에서도 반복된다.
따라서 처음 반복이 일어나는 시점의 인덱스 값을 따로 저장하고 다음 루프부터는 해당 인덱스부터 버블 연산을 수행한다.
2. 선택 정렬
- $O(n^2)$
- 최솟값 또는 최댓값을 찾고 남은 정렬 부분의 가장 앞에 있는 데이터와 swap 연산 수행
💡 min 또는 max 값을 뽑아서 정렬!
def selection_sort(array):
for i in range(len(array)):
target = array[i]
target_idx = i
for j in range(i + 1, len(array)):
if target > array[j]:
target = array[j]
target_idx = j
array[i], array[target_idx] = target, array[i]
return array- 앞에서 부터 정렬된 데이터를 채워나감
3. 삽입 정렬
- $O(n^2)$
- 삽입할 데이터를 이전 데이터들(정렬된 데이터)에 끼워넣는 방법
def insertion_sort(arr):
for i in range(1, len(arr)):
for j in range(i, 0, -1):
if arr[j - 1] > arr[j]:
arr[j - 1], arr[j] = arr[j], arr[j - 1] # swap
else:
break
return arr
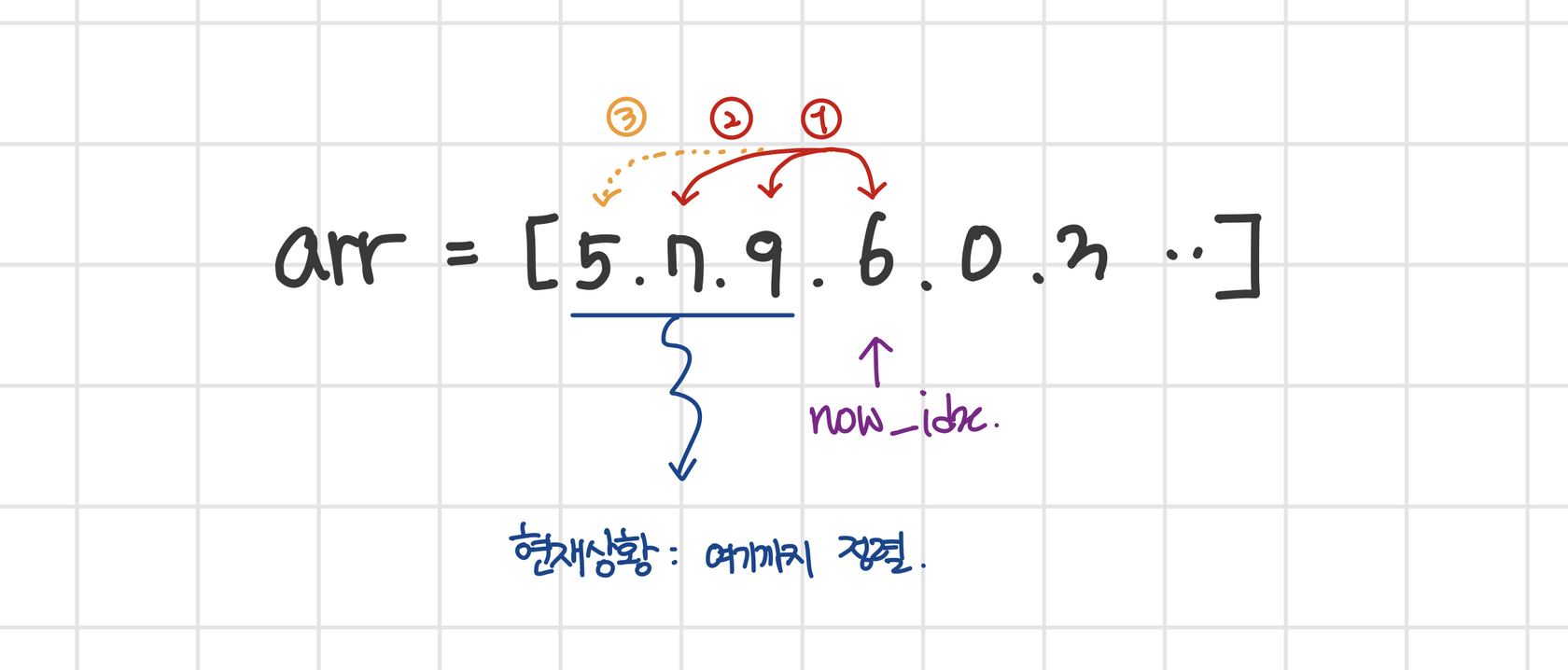
- target 값 : arr[now_idx]
- target 값을 앞으로 옮기다가 더 이상 옮기지 않아도 될 때, stop
- 앞에 있는 배열은 이미 정렬된 상태이기 때문
4. 셸 정렬
- 삽입 정렬의 장점은 살리고 단점은 보완
- unstable 한 방법
- $O(n^{1.25})$
- 삽입 정렬의 장단점
- 장점 : 이미 정렬을 마쳤거나 정렬이 거의 끝나가는 상태에서는 속도가 빠름
- 단점 : 삽입할 위치가 멀리 떨어져 있으면 이동 횟수 증가
- 정렬할 배열의 원소를 그룹으로 나눠 각 그룹별로 정렬을 수행한다.
- 그 후 정렬된 그룹을 합치는 작업을 반복하여 원소의 이동 횟수를 줄인다.
def shell_sort(arr):
n = len(arr)
gap = n // 2
while gap > 0: # gap을 바꿔서 다시 루프 수행
for i in range(gap, n): # 그룹별 정렬 수행
j = i - gap # pair : (j, i)
tmp = arr[i]
5. 퀵 정렬
- pivot을 기준으로 원소의 대소 관계 파악
- pivot을 기준으로 작은 수는 왼쪽에, 큰 수는 오른쪽에 정렬한다.
- 분할 정복, 재귀 사용
- 병합 정렬 🆚 퀵 정렬
- (병합 정렬) 항상 정 가운데를 기준으로 분할
- (퀵 정렬) 임의의 기준값
- 병합 정렬은 단순 분할 후 병합 시점에서 값비교 연산 수행
- 퀵 정렬은 분할 시점부터 비교 연산 수행
파이썬 기반 퀵 정렬
def quick_sort(array):
if len(array) <= 1:
return
pivot = array[len(array) // 2]
lesser_array, equal_array, greater_array = [], [], []
for a in array:
if a < pivot: lesser_array.append(a)
elif a == pivot: equal_array.append(a)
else: greater_array.append(a)
return quick_sort(lesser_array) + equal_array + quick_sort(greater_array)- pivot 값을 기준으로 왼쪽 리스트, 오른쪽 리스트에 원소를 담는다.
- 매번 재귀 호출 시마다 새로운 리스트를 생성해서 리턴 → 메모리 사용 측면에서 비효울적
partition을 이용한 퀵 정렬
def quick_sort(array, start, end):
if start >= end:
return
pivot = start
left = start + 1
right = end
# partition
while left <= right:
while left <= end and array[left] <= array[pivot]:
left += 1
while right > start and array[right] >= array[pivot]:
right -= 1
if left > right:
array[right], array[pivot] = array[pivot], array[right]
else:
array[left], array[right] = array[right], array[left]
quick_sort(array, start, right - 1)
quick_sort(array, right + 1, end)- pivot 값을 기준으로 left, right를 나눠서 데이터를 담는다.(파티션)

- pivot 선택 방법
- pivot 선택 방법은 퀵 정렬의 실행 효율에 큰 영향을 미침
- 배열에서 3개의 원소를 꺼내서 그 중앙값을 pivot으로 설정한다.
- 시간 복잡도
- $O(n lgn)$
- 초깃값이나 pivot 선정에 따라 최악의 경우 $O(n^2)$이 될 수도 있다.
- 원소 수가 적은 경우에는 그다지 빠른 알고리즘이 아니다.
- 공간 복잡도
- $O(n)$
6. 병합 정렬
- 배열을 앞부분과 뒷부분의 그룹으로 나누고 각각을 정렬한 후 병합한다.
- 재귀
- 시간 복잡도 : $O(n lgn)$
buff = [None] * len(array) # 작업용 배열
def merge_sort(arr, left, right):
if left < right:
center = (left + right) // 2
merge_sort(arr, left, center) # 배열의 앞 부분 병합된 상태
merge_sort(arr, center + 1, right) # 배열의 뒷 부분 병합된 상태
p = j = 0 # buff의 포인터
i = k = left # arr의 포인터
# 원본 배열(arr)를 수정하기 위해 배열의 앞부분을 모두 buff로 복사한다.
while i <= center:
buff[p] = arr[i]
p += 1
i += 1
# 배열 arr의 뒷부분(arr[center + 1:]과 앞부분(현재 buff에 있는 상태)의
# 각 원소를 비교해가며 정렬을 수행하여 다시 arr를 채워넣는다.
while i <= right and j < p:
if buff[j] <= arr[i]:
arr[k] = buff[j]
j += 1
else:
arr[k] = arr[i]
i += 1
k += 1
# 만약 buff가 남았다면 모든 원소가 arr의 뒷부분보다 크다는 뜻 이므로
# 해당 부분은 그냥 arr 맨 뒤에 붙여준다.
while j < p:
arr[k] = buff[j]
k += 1
j += 1
💡 heapq.merge(arr1, arr2)
# 정렬된 상태의 두 배열
a = [2, 4, 6, 8, 11, 13]
b = [1, 2, 3, 4, 9, 16, 21]
c = list(heapq.merge(a, b))
- 정렬된 두 배열에 대한 병합 정렬을 heapq.merge() 를 이용해서 구현할 수 있다.
7. 힙 정렬
- 힙(heap) : ‘부모의 값이 자식의 값보다 항상 크다’는 조건을 만족하는 완전 이진 트리
- 항상 부모 > 자식 : max heap
- 항상 자식 > 부모 : min heap
- 힙의 루트에는 최댓값이 자리하게 된다.
- 시간 복잡도 : $O(n lgn)$
- 원소 개수만큼 선택 정렬 수행 : $O(n)$
- 힙으로 만드는 작업 : $O(lgn)$
힙 정렬 구현
- ‘힙의 루트에는 항상 최댓값이 위치한다.’는 특성을 이용해서 구현한다.
- 힙에서 최댓값인 루트를 꺼낸다.
- 루트 이외의 부분을 힙으로 만든다.
⭐ 계속해서 최댓값을 뽑아내므로, 선택 정렬을 응용한 알고리즘이다.

힙은 완전이진트리 성질을 만족하므로 1차원 배열로 표현이 가능하다.
- 힙을 1차원 배열로 나타내기 위한 자식 노드 위치 표현
left_idx = 2 * idx + 1
right_idx = 2 * idx + 2def heap_sort(arr):
# left ~ right 힙으로 만들기
def down_heap(arr, left, right):
temp = arr[left] # 루트 노드
parent = left
while parent < (right + 1) // 2:
cl = parent * 2 + 1 # 왼쪽 자식
cr = cl + 1 # 오른쪽 자식
child = cr if cr <= right and arr[cr] > arr[cl] else cl # 더 큰 자식
if temp >= arr[child]: # 루트 노드 그대로 유지 가능
break
arr[parent] = arr[child] # 루트 노드와 자식 노드 교환 필요
parent = child # 루트 노드 인덱스와 자식 노드 인덱스 교환
arr[parent] = temp
n = len(arr)
# arr[i] ~ arr[n - 1]을 힙으로 만들기
for i in range((n - 1) // 2, -1, -1):
down_heap(arr, i, n - 1)
for i in range(n - 1, 0, -1):
# 최댓값인 arr[0]와 마지막 원소를 교환
arr[0], arr[i] = arr[i], arr[0]
# arr[0] ~ arr[i - 1]을 힙으로 만들기
down_heap(arr, 0, i - 1)
8. 도수 정렬
- 원소의 대소 관계를 판단하지 않고 빠르게 정렬하는 알고리즘
- 각 원소가 몇개 있는 가를 나타내는 누적 도수 분포표를 만든다.
# 모든 범위를 포함하는 리스트 선언(모든 값은 0으로 초기화)
count = [0] * (max(array) + 1)
for i in range(len(array)):
count[array[i]] += 1 # 각 데이터에 해당하는 인덱스 값 증가
for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
for j in range(count[i]):
print(i, end=' ')- 대신 수의 범위가 매우 적을 때만 사용할 수 있다.
- 인덱스를 사용해야하므로 수의 범위가 양수로 한정된다.
Stable Sort 🆚 Unstable Sort
- Stable Sort
- 정렬 전과 후 순서를 동일하게 유지하는 것
- Bubble Sort(버블 정렬)
- Insertion Sort(삽입 정렬)
- Merge Sort(합병 정렬)
- Unstable Sort
- Selection Sort(선택 정렬)
- Quick Sort(퀵 정렬)
- Heap Sort(힙 정렬)
📝 Note
- 면접 빈출 정렬 알고리즘 : quick sort, merge sort
- 알고리즘에 대한 정확한 원리를 알고 있는 게 중요
- typing.MutableSequence
- type을 나타내는 엘리어스
- mutable 자료형을 나타냄
🔗 Reference
- collections.abc — 컨테이너의 추상 베이스 클래스 — Python 3.11.0 문서
- typing --- 형 힌트 지원 — 파이썬 설명서 주석판
- 힙 정렬(Heap Sort) · ratsgo's blog
728x90
'🌱 Dev Diary > 📄 TIL' 카테고리의 다른 글
| 알고리즘 이론 - 스택 (0) | 2022.11.05 |
|---|---|
| Week01 TEST (0) | 2022.11.05 |
| 알고리즘 이론 - 재귀 (0) | 2022.11.03 |
| 파이썬 알고리즘 기초 점검 / 정리 (0) | 2022.10.30 |
| Mini Project (0) | 2022.10.30 |
