728x90
☑️ To-do
- 재귀 알고리즘 정리하기
- 하노이의 탑 로직 완벽 이해하기
- N-Queens 로직 완벽 이해하기
- CSAPP Ch 1.3 까지 정리하기
재귀(Recursion)
- 팩토리얼 함수로 구현하기
def factorial(n: int) -> int:
if n > 0:
return n * factorial(n - 1)
else:
return 1- math.factorial() : 인자가 정수가 아니거나 음수가 들어오면 ValueError 예외 처리를 내보낸다.
직접 재귀(direct)
- 자신과 동일한 함수를 호출하는 방식
간접 재귀(indirect)
- a( ) 가 b( ) 호출 ↔ b( ) 가 a( ) 호출
유클리드 호제법
- GCD를 재귀적으로 구하는 방법
- math 모듈에서는 math.gcd(integers) 로 사용 가능하다!
- 큰 값을 작은 값으로 나누어 떨어지면 작은 값이 최대 공약수가 된다.
y가 0이면 -> x
y가 0이 아니면 -> gcd(y, x % y)
def gcd(x, y): # x : 큰 수, y : 작은 수
if y == 0:
return x
else:
return gcd(y, x % y)💡 직사각형의 작은 변을 기준으로 나누는 로직 생각하기!
재귀 알고리즘 분석
def recur(n):
if n > 0:
recur(n - 1)
print(n)
recur(n - 2)하향식 분석
- 가장 상위 함수부터 호출을 시작해서 계단식으로 자세히 조사해 나가는 분석 방법
- 맨 위부터 분석하면 같은 함수를 여러 번 호출할 수 있어 무조건 효율적인 방법은 아니다.
상향식 분석
- 맨 아래 함수부터 쌓아 올리며 분석하는 방법
하노이의 탑
def hanoi(num, a, b, c):
if num == 1:
return
hanoi(num - 1, a, c, b)
hanoi(num - 1, b, a, c)hanoi(n, a, b, c)- n : 원반 개수
- a : 출발 기둥
- b : 중간 기둥
- c : 도착 기둥
원판 n개가 주어졌을 때,
1. n - 1개의 원판 묶음을 중간 기둥(b)으로 옮기고 맨 아래 원판을 최종 도착 기둥(c)으로 옮긴다.
2. 이후 현재 중간 기둥(b)에 위치한 n - 1개의 기둥을 최종 도착 기둥(c)로 옮긴다.
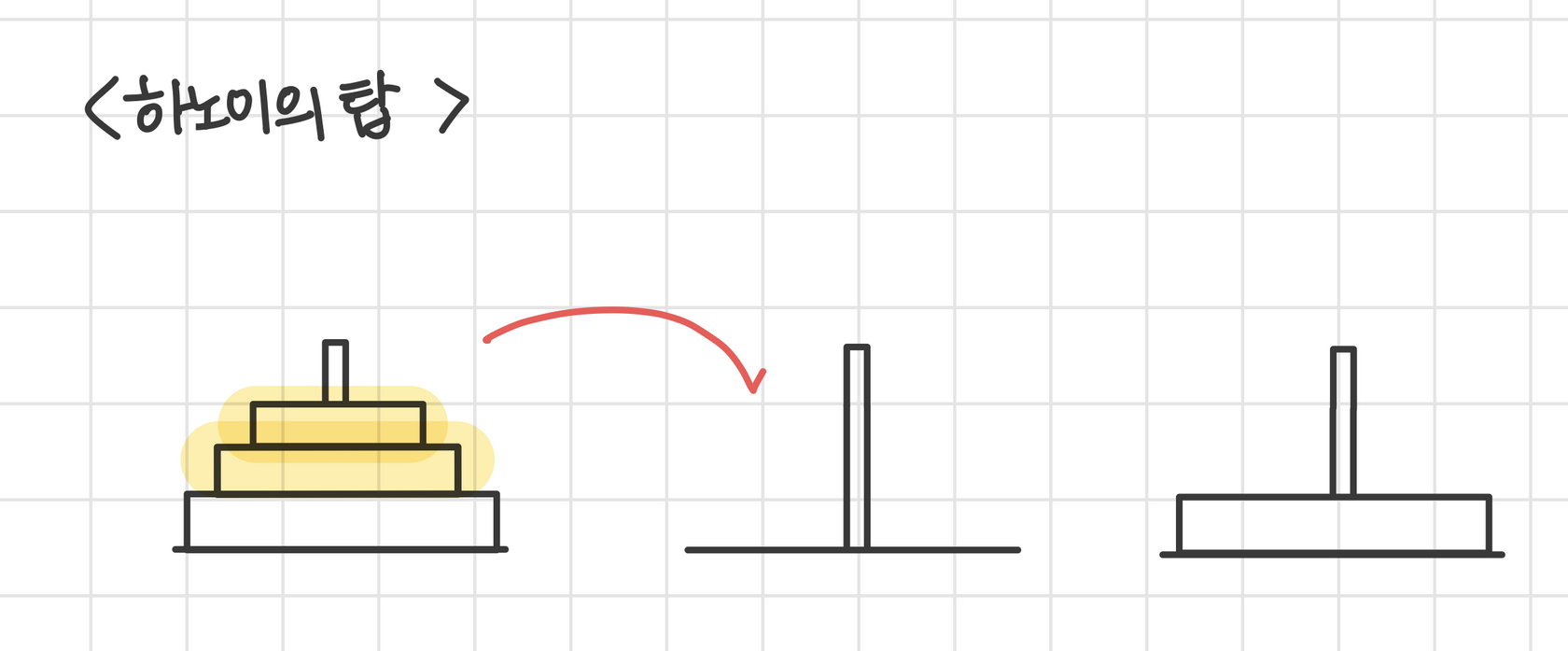
✨ 핵심 IDEA
- 가장 큰 원판을 옮기기 위해서는 n - 1개의 원판을 temp 기둥으로 옮겨야하고 이 n - 1개의 원판을 모두 옮기고 나서는 또 다시 이 n - 1개의 원판도 최종 기둥으로 옮겨야 하므로 또 다시 재귀를 시작한다.
하노이 탑의 점화식
- n = 1, 1번
- n = 2, 3번
- n = 3, 7번
- n = 5, 15번
→ $2n^2 - 1$
boj. 1914
- Try 1 시간초과
import sys
input = sys.stdin.readline
n = int(input())
answer = 0
order_ans = []
def hanoi(flag, num, start, end):
global answer
answer += 1
temp = 6 - end - start
if num == 1:
if flag: order_ans.append('{} {}'.format(start, end))
return
else:
hanoi(flag, num - 1, start, temp)
if flag: order_ans.append('{} {}'.format(start, end))
hanoi(flag, num - 1, temp, end)
if n <= 20:
hanoi(1, n, 1, 3)
print(answer)
print('\\n'.join(order_ans))
else:
hanoi(0, n, 1, 3)
print(answer)이런식으로 문제에서 제시된 대로 원판의 개수가 20이하의 경우에는 hanoi() 함수를 돌려서 나온 횟수만을 출력해주도록 구현을 했는데 시간초과가 났다.
알고 보니, 원판의 개수가 20보다 큰 경우에는 점화식만을 출력해주면 되는 문제였다.
결국은 점화식을 알고 있느냐의 문제…
- Try 2 통과
import sys
input = sys.stdin.readline
n = int(input())
answer = 0
order_ans = []
def hanoi(num, a, b, c):
if num == 1:
print(a, c)
return
hanoi(num - 1, a, c, b)
print(a, c)
hanoi(num - 1, b, a, c)
print(2 ** n - 1)
if n <= 20: hanoi(n, 1, 2, 3)
N-Queen
boj. 9663
n = int(input())
ans = 0
row = [-1] * n
# row[x] (x행)에 퀸을 놓는 경우 유효성 검사
def backtracking(x):
# 이전 행을 돌면서 놓인 퀸 위치 중 같은 행 또는 열, 대각선이 있는 지 검사
# 이전 행을 검사하는 이유? - 이전 행은 이미 유효한 위치이기 때문
for i in range(x):
if row[x] == row[i] or abs(row[x] - row[i]) == abs(x - i): # 같은 col, 대각선 검사
return False
return True
def n_queens(x):
global ans
if x == n: # n개의 퀸을 모두 놓았을 경우 ans++
ans += 1
else:
for i in range(n): # row check (열 순회)
row[x] = i
if backtracking(x): # 유효하면 다음 스텝으로 넘어감
n_queens(x+1) # 다른 row 검사(행 순회)
n_queens(0)
print(ans)- python 으로는 통과가 안되고 pypy 로 밖에 통과가 안되는 문제
- 백트래킹으로 현재 탐색 중인 위치에 퀸을 놓는 게 가능한지 검사한다.
- 이 문제에서 유의할 점은 2차원의 체스판이라고 해서 2차원 배열을 이용해서 퀸 위치를 파악하는 것이 아니라 1차원 배열로 row와 column의 위치를 모두 표시한다.
- 만약 row[a] = b 라면 체스판의 a행 b열에 체스판을 놓을 수 있다는 뜻이다.
728x90
'🌱 Dev Diary > 📄 TIL' 카테고리의 다른 글
| 알고리즘 이론 - 스택 (0) | 2022.11.05 |
|---|---|
| Week01 TEST (0) | 2022.11.05 |
| 알고리즘 이론 - 정렬 (1) | 2022.11.03 |
| 파이썬 알고리즘 기초 점검 / 정리 (0) | 2022.10.30 |
| Mini Project (0) | 2022.10.30 |
