728x90
탐색
선형 탐색 알고리즘(Linear Search Algorithm)
- 최선의 경우 : 1
- 최악의 경우 :O(n)
이진 탐색 알고리즘(Binary Search Algorithm)
📢 정렬된 자료일 경우에만 사용 가능하다.
- 최선의 경우 : 1
- 최악의 경우 :log2n
재귀 함수
- base case : 문제가 이미 충분히 작아서 바로 풀 수 있는 경우
- recursive case : 문제를 더 작은 문제로 쪼개서 풀 수 있는 경우(재귀)
- 반복문으로 풀 수 있는 문제는 재귀 함수로 풀 수 있다.
- 재귀 함수의 문제점
- call stack이 너무 많이 쌓이게 되면 프로그램 과부하 발생
- 재귀 함수의 호출이 너무 많이 발생하면 반복문으로 푸는 게 좋음
알고리즘 패러다임
Brute-Force Attack(무차별 대입 공격)
- input이 커질 수록 더욱 비효율적
- 무차별로 가능한 모든 방법을 대입해보는 것
- 가장 순진한 알고리즘 접근법
장점
- 직관적이고 명확함
- 답을 확실하게 찾을 수 있음
단점
- input이 커질 수록 비효율적임
Divide and Conquer (분할 정복)
- Divide : 문제를 부분 문제로 나눈다.
- Conquer : 각 부분 문제를 정복한다.Base Case (문제가 충분히 작아진 상태) 까지 분할 정복 반복
- Combine : 부분 문제들의 솔루션을 합쳐서 기존 문제를 해결한다.
정렬

- Sorting Algorithm Comparision Simulation
Sorting Algorithms Animations
Animation, code, analysis, and discussion of 8 sorting algorithms on 4 initial conditions.
www.toptal.com
선택 정렬(Selection Sort)
- 정렬이 안된 요소들 중 최소값을 선택해 배열의 첫 번째 요소와 교환한다.
- 각 위치에 어떤 값이 들어갈 지 찾는다.
- O(n^2)
삽입 정렬(Insertion Sort)
- 정렬이 안된 요소들을 앞의 정렬된 요소들과 비교해 적절한 위치를 찾아 삽입한다.
- 각 값이 어떤 위치에 들어갈 지 찾는다.
- O(n^2)
합병 정렬(Merge Sort)
- Divide : 리스트를 반으로 나눈다.
- Conquer : 왼쪽 리스트와 오른쪽 리스트를 각각 정렬한다.
- Combine : 정렬된 두 리스트를 하나의 정렬된 리스트로 합병한다.
퀵 정렬(Quicksort)
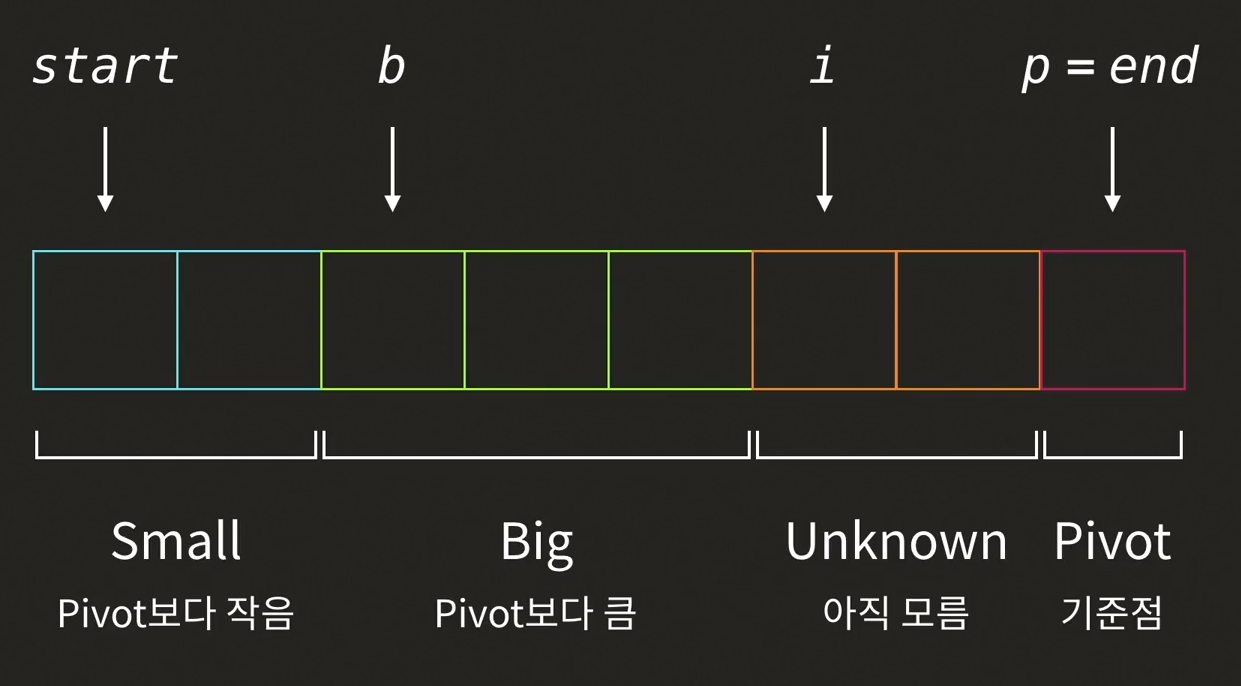
- Divide : Partition(⭐핵심과정) - pivot 값 선정
- Conquer : Pivot 보다 작은 값들을 왼쪽에 정렬, Pivot 보다 큰 값들을 오른쪽에 정렬Pivot을 기준으로 값 그룹화
- Unknown 그룹을 이분법적으로 나눠 Small 그룹과 Big 그룹으로 분류
- b 인덱스와 i 인덱스를 증가시켜가며 진행
탐욕 알고리즘(Greedy Algorithm)
- 미래를 내다보지 않고, 당장 눈 앞에 보이는 최적의 선택을 하는 방식
장점
- 간단하고 빠르다.
단점
- 최적의 답이 보장되지 않는다.
When?
- 탐욕 알고리즘 이외의 알고리즘이 매우 느린 경우 사용한다.
- 최적의 답이 필요 하지 않을 때 사용한다.
- 탐욕 알고리즘이 최적의 답을 보장해주는 경우 사용한다.
최적 부분 구조(Optimal Substructure)
: 부분 문제들의 최적의 답을 이용하여 기존 문제의 최적의 답을 구할 수 있다는 것
부분 문제를 만들 수 있으며 부분 문제의 최적화된 값이 전체 결과까지 최적화된 값을 주는가?
탐욕적 선택 속성(Greedy Choice Property)
: 각 단계에서 탐욕스런 선택이 최종 답을 구하기 위한 최적의 선택
당장의 상황에서 목표를 위해 가장 도움이 되는 것이라고 할만한 것을 고를 수 있는가?
💡 최적 부분 구조와 탐욕적 선택 속성이 있는 경우 탐욕 알고리즘이 최적의 선택이 된다.
💡 두 속성은 분리될 수 있으며 둘 중 하나만 충족하는 경우도 있다.
728x90
'📊 Algorithm > Paradigm' 카테고리의 다른 글
| [Python Plus] Extended Slices [::-1] (0) | 2022.01.25 |
|---|---|
| [알고리즘 대비 - 이코테] 3. 구현 (0) | 2021.09.19 |
| [알고리즘 대비 - 이코테] 2. 그리디 (0) | 2021.08.20 |
| [알고리즘 대비 - 이코테] 1. 자료형 (0) | 2021.06.02 |
| [알고리즘 풀이방법] 알고리즘 평가법 (0) | 2021.05.26 |
