728x90
☑️ To-do
- 이진 트리 이론 정리
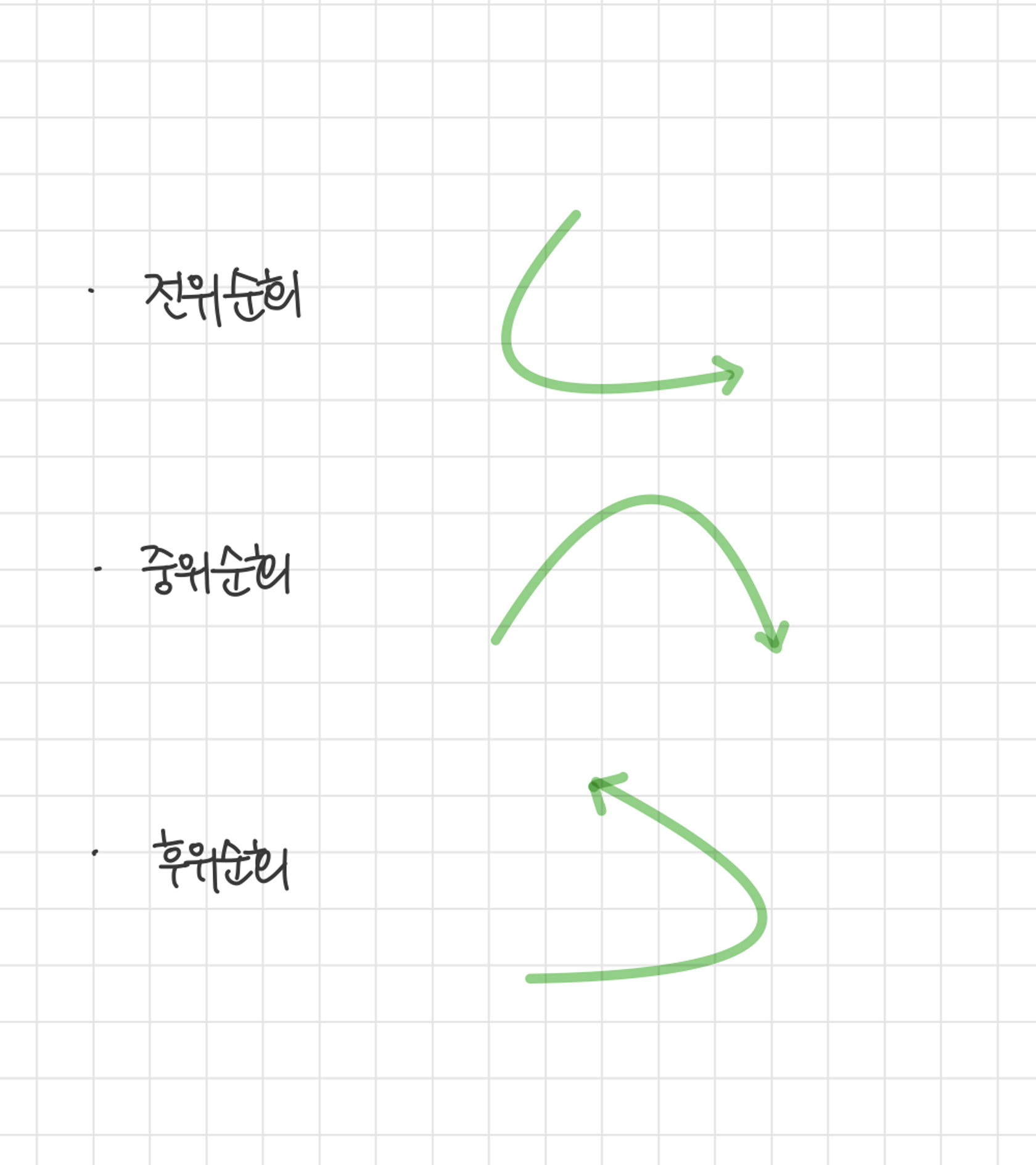
- 전위, 중위, 후위 순회
- Introduction to Algorithms 이진 트리
- Week03 문제 풀이
- 1707 / 21606
이진 트리
- 노드가 왼쪽 자식과 오른쪽 자식만을 갖는 트리
- 자식 노드의 최대 개수는 2이다.
💡 두 자식 가운데 하나 또는 둘 다 존재하지 않는 노드가 있어도 상관없다!
완전 이진 트리
- 루트부터 아래쪽 레벨로 노드가 가득 차 있고, 같은 레벨 안에서 왼쪽부터 오른쪽으로 노드가 채워져 있는 이진 트리
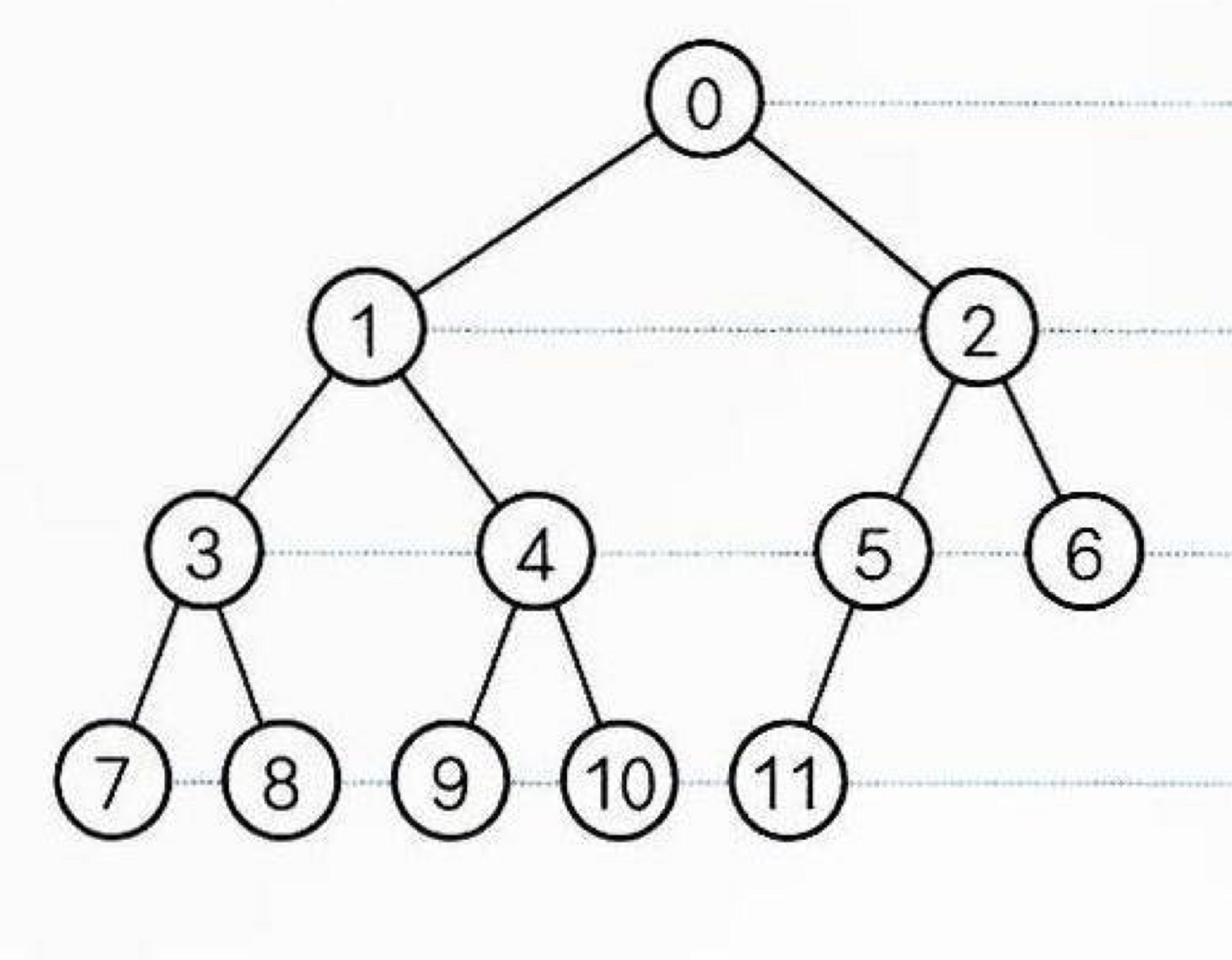
- 마지막 레벨을 제외하고 모든 레벨에 노드를 가득채운다.
- 왼쪽으로 노드들이 치우친 상태
이진 검색 트리(Binary Search Tree)
Field
- key : 키 값
- left : 왼쪽 자식
- right : 오른쪽 자식
- p(parent) : 부모 노드
left_subtree (keys) < node (key) ≤ right_subtree (keys)- 임의의 노드 x에 대해 x의 왼쪽 서브 트리의 키는
x.key보다 크지 않고 x의 오른쪽 서브 트리의 키는x.key보다 작지 않다.
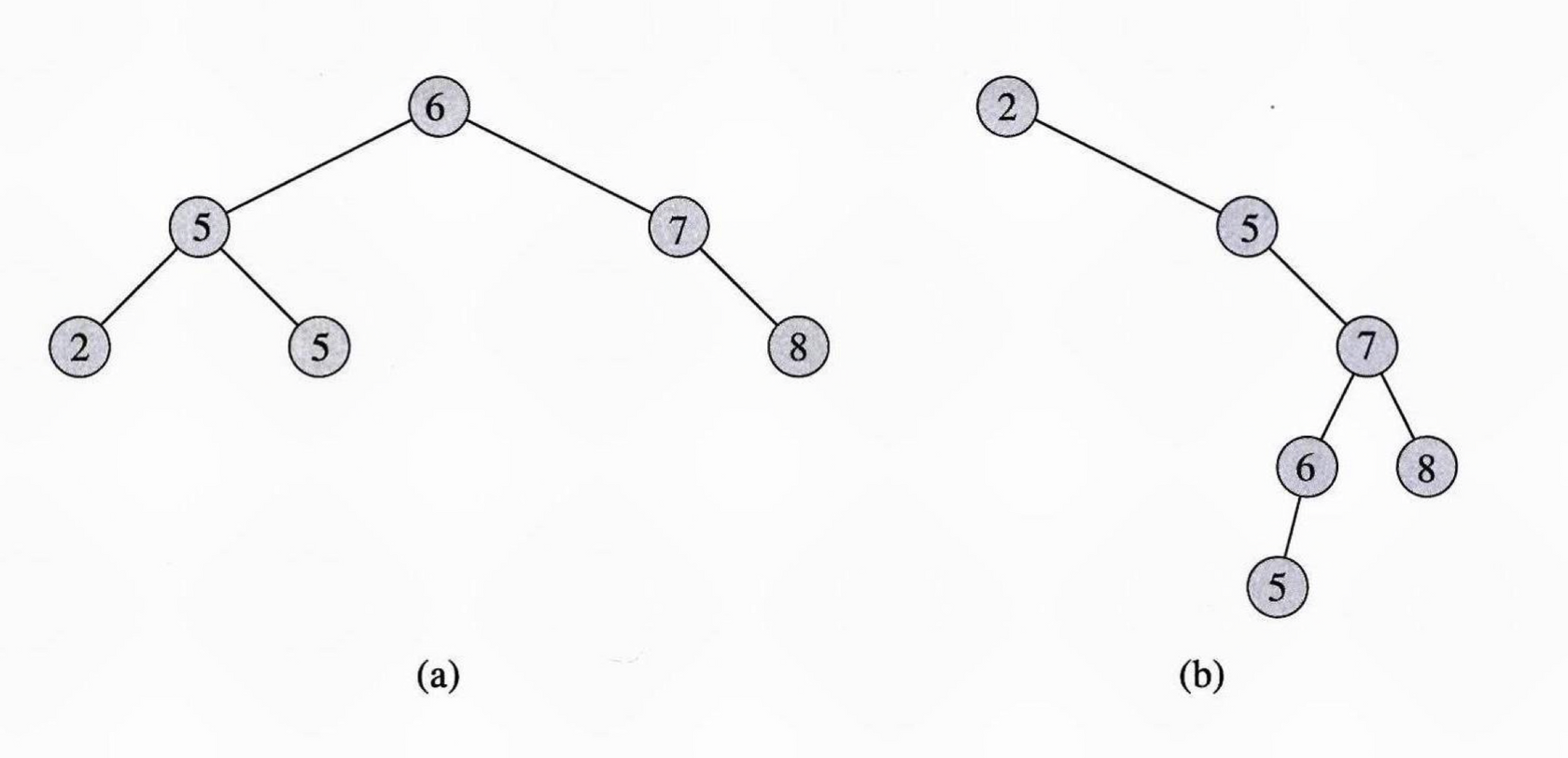
⭐ 같은 값들로 이루어진 집합에 대해 서로 다른 이진 검색 트리가 존재할 수 있다.
- DFS 방식으로
중위 순회로 스캔 하면 노드의 키 값을 오름차순으로 얻을 수 있다. - 루트 노드 : 부모가 NIL인 유일한 노드
장점
- 단순한 구조
- DFS 중위 순회로 오름차순 정렬 값 얻을 수 있음
- 이진 검색과 유사한 방식
- 노드 삽입 용이
중위 트리 순회(Inorder tree walk)
- 초기 호출 이후 트리의 각 노드에 대해 재귀적으로 두 번
- 왼쪽 자식, 오른쪽 자식 - 총 두 번 자기 호출을 수행한다.
- 따라서 선형 시간이 소요된다. $O(n)$
Querying a binary search tree
- MINIMUM
- MAXIMUM
- SUCCESOR
- PREDECESSOR
🙋 같은 키를 가지는 이진 검색 트리?
- 기본적으로 이진 검색 트리는 모두 유일한 키 값을 갖도록 구성하는 걸 기본으로 여긴다.
- 오히려 중복되는 키 값을 갖는 경우에는 균형 검색 트리(self-balancing BSTs)가 더 적합하다.
이진 검색 트리 구현
이진 검색 트리 클래스 Binary Search Tree
def __init__(self):
self.root = None- 노드가 없는 상태로 이진 검색 트리를 초기화한다.
검색
순환적 형태의 이진 트리 검색
def interative_search(self, key):
p = self.root
while True:
if p is None:
return None
if key == p.key:
return p.value
elif key < p.key:
p = p.left
else:
p = p.right1. 루트에서 검색을 시작해, 트리의 단순 경로 하나를 따라 내려간다.
2. 이때 만나게 되는 각 노드의 키(p.key)와 찾으려는 키(key)를 비교한다.
3-1. 두 키가 같으면 검색을 종료한다.
3-2. key가 p.key보다 작으면 검색은 p의 왼쪽 서브 트리를 대상으로 검색을 계속 진행한다.
3-3. 반대로 key가 p.key보다 크면 오른쪽 서브 트리를 대상으로 검색을 계속 진행한다.
재귀적 형태의 이진 트리 검색
def recursive_search(self, key):
p = self.root
if p is None:
return None
if key < p.key:
return recursive_search(p.left, key)
else: return recursive_search(p.right, key)
삽입
⚠️ 노드를 삽입한 뒤에도 트리의 형태가 이진 검색 트리의 조건을 유지해야한다.
이진 트리에 노드 삽입
def add(self, key, value):
def add_node(node, key, value):
if key == node.key:
return False
elif key < node.key:
if node.left is None:
node.left = Node(key, value, None, None)
else:
add_node(node.left, key, value)
else:
if node.right is None:
node.right = Node(key, value, None, None)
else:
add_node(node.right, key, value)
return True
if self.root is None: # 루트 노드가 빈 상태일 경우
self.root = None(key, value, None, None)
return True
else:
return add_node(self.root, key, value)
- x 노드에서 시작해서 None을 찾아, 입력 항목을 key로 변경하기 위해 단순 경로를 따라 내려간다.
- 이때, x의 부모 포인터를 기록하며 내려간다.
- 임의 노드(x)의 루트에 주목한다.
key == x.key
- 삽입을 실패하고 종료한다.
- 이미 키가 존재하므로 값을 넣을 수가 없다.
key < x.key
- 왼쪽 자식 노드가 없으면 그 자리에 노드를 삽입하고 종료한다.
- 왼쪽 자식 노드가 있으면 주목 노드를 왼쪽 자식 노드로 옮긴다. (↩️ 다시 재귀 수행)
key > x.key
- 오른쪽 자식 노드가 없으면 그 자리에 노드를 삽입하고 종료한다.
- 오른쪽 자식 노드가 있으면 주목 노드를 오른쪽 자식 노드로 옮긴다. (↩️ 다시 재귀 수행)
삭제
이진 트리에서 노드 삭제
'''
@p : 현재 스캔 중인 노드
@parent : p의 부모 노드
@is_left_child : p가 parent의 왼쪽 자식 노드인지
'''
def remove(self, key):
p = self.root
parent = None
is_left_child = True
# 삭제하려는 노드 검색
while True:
if p is None: # 해당 키가 트리 내에 존재하지 않음
return False
if key == p.key: # 키와 동일한 노드 검색 완료
break
else:
parent = p # 가지를 내려가므로 부모 노드의 포인터를 자식 노드로 변경
if key < p.key:
is_left_child = True
p = p.left
else:
is_left_child = False
p = p.right
# CASE 2
if p.left is None: # 왼쪽 자식이 없는 경우 / CASE 1이 이루어지는 부분
if p is self.root:
self.root = p.right
elif is_left_child:
parent.left = p.right
else:
if p is self.root:
self.root = p.right
elif is_left_child:
parent.left = p.right
else:
parent.right = p.right
elif p.right is None: # 오른쪽 자식이 없는 경우
if p is self.root:
self.root = p.left
elif is_left_child:
parent.left = p.left
else:
parent.right = p.left
# CASE 3
else:
parent = p
left = p.left
is_left_child = True
while left.right is not None: # 왼쪽 서브트리 내에서 가장 큰 노드를 검색
parent = left
left = left.right
is_left_child = False
p.key = left.key # swap
p.value = left.value
if is_left_child:
parent.left = left.left
else:
parent.right = left.left
return True- Case 1. 자식 노드가 없는 노드를 삭제하는 경우
- 1.삭제할 노드가 부모 노드의 왼쪽 자식이면, 부모의 왼쪽 포인터를 None으로 변경한다.
- 2.삭제할 노드가 부모 노드의 오른쪽 자식이면, 부모의 오른쪽 포인터를 None으로 변경한다.
- 💡 찾는 자식 노드가 단말 노드이므로 부모 노드의 포인터(left or right)만 변경해주면 된다.

- Case 2. 자식 노드가 1개인 노드를 삭제하는 경우
- 1.삭제할 노드가 부모 노드의 왼쪽 자식이면, 부모의 왼쪽 포인터를 삭제할 노드의 자식으로 변경한다.
- 2.삭제할 노드가 부모 노드의 오른쪽 자식이면, 부모의 오른쪽 포인터를 삭제할 노드의 자식으로 변경한다.
- Case 3. 자식 노드가 2개인 노드를 삭제하는 경우
- 1. 삭제할 노드의 왼쪽 서브트리에서 키값이 가장 큰 노드를 검색한다.
- 2. 검색한 노드를 삭제 위치로 옮긴다. 즉 검색한 노드의 데이터를 삭제할 노드 위치에 복사한다.
- 3. 옮긴 노드를 삭제한다.
- 이때, 옮긴 노드에 자식이 없으면 Case1 을, 자식이 1개만 있으면 Case2 를 수행한다.
➕ Plus
- 파이썬 자료형 클래스로 선언할 때 생성자 자동으로 생성하기
def __init__(self) -> None:
pass
728x90
'🌱 Dev Diary > 📄 TIL' 카테고리의 다른 글
| C 정복하기(2) - 메모리 할당 (0) | 2022.11.28 |
|---|---|
| C 정복하기(1) - 포인터 (0) | 2022.11.28 |
| 알고리즘 이론 - 그래프 이론 기본 (0) | 2022.11.16 |
| Week02 TEST (0) | 2022.11.12 |
| 알고리즘 이론 - 이분 탐색 (0) | 2022.11.10 |
